Archives

Using JavaScript to locate controls in ASP.net pages that are linked to master pages can be tricky.  This is because the ASP.net reassigns control IDs dynamically and the names change.

A simple solution is to use asp.net inline Tags.

For Example:

Instead for using:

document.getElementById(“Label1″)

try using:

document.getElementById(“<%=Label1.ClientID%>”)

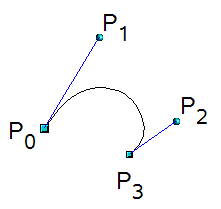
The Bezier Curve formula below can be used to define smooth curves between points in space using line handlers (line P0 to P1 and line P2 to P3).

P(t) = (1-t)^3P0 + 3(1-t)^2tP1 + 3(1-t)t^2P2 + t^3P3

At  t=0 you will be at p0, and at t=1 you will be at p3.

The function below is a C# implementation of the formula return the X and Y coordinates of a position on the curve for a given Time (t) and the 4 points that define the Bezier Curve.    

You can easily extend this to connect multiple curves to each other (multi-segmented path). You can do this simply by making p0 of subsequent segments equal p3 of the prior segment.

Include this function in your c# projects to create smooth curves.

C# Code Sample:

private Vector2 GetPoint(float t, Vector2 p0, Vector2 p1, Vector2 p2, Vector2 p3)
{
  float cx = 3 * (p1.X - p0.X);
  float cy = 3 * (p1.Y - p0.Y);
  float bx = 3 * (p2.X - p1.X) - cx;
  float by = 3 * (p2.Y - p1.Y) - cy;
  float ax = p3.X - p0.X - cx - bx;
  float ay = p3.Y - p0.Y - cy - by;
  float Cube = t * t * t;
  float Square = t * t;

  float resX = (ax * Cube) + (bx * Square) + (cx * t) + p0.X;
  float resY = (ay * Cube) + (by * Square) + (cy * t) + p0.Y;

  return new Vector2(resX, resY);
}

To use the function, simply pass in the 4 point and a time (between 0 and 1).  To draw the curve, try calling this function from a for loop that looks something like this:

// preset your p0,p1,p2,p3

Vector2 PlotPoint;
for (float t = 0;  t <= 1.0f; t += 0.01f)
{
   PlotPoint = GetPoint(t, p0, p1, p2, p3);

   // now call some function to plot the PlotPoint
   YourDrawFunction(PlotPoint);
}

This basically starts you at p0 when time t is zero and at each increment of time +0.01 you will slowly move on the curve towards p3.

So to give you an idea of how this was used by my son in one of his games, watch the video below

• Note these are circular Paths each withe 3 segments. Each segment is a 4 point Bezier calculation.
• p3 of the each segment is common to p0 of next each segment.
• To make the circular, p3 of last segment must be same as p0 of 1st segment.
• p2 and p3 of each segment must be on a strait line with p0 and p1 or the next segment. (this give you the double handles for each point)

So this means:

• If a path point was moved by user, you must also move left and right control handler points by same deltas
• If left handler moved, must also move corresponding path point so it intersects line to other handler at mid point
• If right handler moved, must also move corresponding path point so it intersects line to other handler at mid point

Good luck